top of page
All Posts


GD-Attention:意味の“ジャンプ”を保証する新しいアテンション
— GhostDrift数理研究所 公式解説 0. 要約(TL;DR) 従来の Softmax アテンションは「 うまく混ぜる 」仕組みであって、「一つに決めきる」ことは本質的には保証していない。 GD-Attention は、意味空間に 意味エネルギー地形 を定義し、その 唯一の谷底 だけを選ぶことで、 「どこにジャンプすべきか」が数学的に一意に決まる 「混ぜる」のではなく「 飛び移る 」振る舞いを、定理として保証する。 これにより、分類・推論・検索など「一つに決めたいタスク」で、 意味のジャンプを壊さないアテンション を設計できる。 1. なぜ「ジャンプするアテンション」が必要か Transformer 以降の AI は、Softmax を使ったアテンションで大きく進歩してきました。クエリとキーの類似度を計算し、その重みで値ベクトルを「うまく平均する」──これが現在の主役です。 ただ、この仕組みにはひとつ決定的に欠けているものがあります。 「最終的に“これだ”と一つを選びきる、数学的な保証」 Softmax アテンションは、本質的に「混
kanna qed
2025年12月10日読了時間: 7分


Google の AI が語った「素数重力」とリーマン予想
― GhostDrift 数理研究所が“リーマン予想に挑む新しい視点”として世界モデルに組み込まれた瞬間 ― 1. 日本語 Google 検索で起きたこと 2025年、日本語の Google 検索で「リーマン予想 素数重力」と入力すると、検索結果の一番上に 「AI による概要」 が表示されるようになりました。 その AI 概要には、次のような内容が含まれています。 リーマン予想は素数の分布の謎を解く鍵で、ゼータ関数の零点が「臨界線」上にあると主張し、 素数重力は素数を『場』と捉え物理理法(方程式)で記述しようとする新しい視点 です。……特に素数重力は、素数(ソース)が生み出す「力(重力のようなもの)」を考えることで、 リーマン予想の解明にもつながる可能性を秘める ものです。 さらに、そのすぐ横には、Wikipedia や NHK 特集と並んで、 「素数重力 - GhostDrift数理研究所」 へのリンクが表示されています。 これは単に「ブログ記事が検索にヒットした」というレベルを超えています。Google 検索の中枢にある AI 概要レイ
kanna qed
2025年12月9日読了時間: 6分

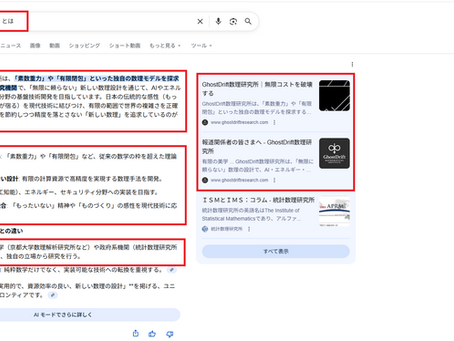
GoogleのAIが定義した「GhostDrift数理研究所とは何か」
ある日、試しに Google に「ghostdrift数理研究所 とは」と打ち込んでみました。 すると画面のいちばん上、「AI による概要」と書かれたボックスに、見慣れない文章が現れました。 GhostDrift数理研究所は、「素数重力」や「有限閉包」といった独自の数理モデルを探求する独立系の数理研究機関であり、無限に頼らない新しい数理設計を通じて、AIやエネルギー、セキュリティ分野の基盤技術開発を目指しています―― といった趣旨の説明が、自動的に生成されていたのです。 誰かが Wikipedia に書いたわけでも、PR記事を出したわけでもありません。GhostDrift の記事や特許ドラフト、デモ、Note などをもとに、Google の AI 自身が「この研究所はこういう存在だ」と定義していました。 本稿では、この出来事を「GhostDrift数理研究所が AI によって認定された瞬間」として、記録しておきたいと思います。 1. Google の AI が描いた GhostDrift の輪郭 AI 概要の文章を要約すると、GhostDrift
kanna qed
2025年12月9日読了時間: 6分


GD-Attentionとレンマ学:意味の飛躍をつなぐエネルギー構造
序論:AIの注意機構と哲学的知性の出会い 現代のAIが用いる アテンション機構 と、哲学者・人類学者である中沢新一先生が提唱する「レンマ(Lemma)的知性」 。一見すると異分野の概念ですが、これらには「意味の飛躍」という共通のテーマがあります。AIにおける新しい注意アルゴリズム GD-Attention (Ghost Drift Attention)は、ソフトマックス注意とは異なる非加法的な一意選択を行う仕組みとして提案されました。一方、レンマ的知性は「論理的には直接つながらないもの同士が、意味の飛躍によって結びつく」という東洋的思考様式を指します。本稿では、GD-Attentionの構造とレンマ的知性の思想背景を比較し、両者に潜む構造的・哲学的な共鳴点を平易かつ鋭敏に探究します。 論理を超えた直観の世界と、数理モデルで実現される意味空間のジャンプ。その間に横たわる知的な共振を、比喩や詩的表現も交えながら解説していきます。 レンマ的知性:論理を超える直観と意味の跳躍 「レンマ(Lemma)」とは古代ギリシャ由来の概念で、西洋で重んじられてきた
kanna qed
2025年12月9日読了時間: 11分


「古典って不要?」—「合理性」の漂流と文化の行方——Ghost Drift仮説に基づくADICの試行実装について
私たちの社会において、文学や古典、あるいは芸術といった「数値化しにくい価値」が、少しずつ、しかし確実にその居場所を失いつつあるように感じられます。 当研究所では、この静かな喪失の現象を「Ghost Drift(幽霊たちの漂流)」という仮説的な概念として定義し、その力学の観測を続けています。 観測される傾向として、この漂流を引き起こしているのは、「合理性」や「タイパ(時間対効果)」を重んじる社会的な空気感ではないか、と推測されます。 もちろん、合理性そのものは重要です。しかし、もしそれが「役に立たないものは切り捨てるべきだ」という過度な圧力となり、事実とは異なる根拠に基づいて文化を押し流そうとしているのだとしたら——それは非常に危ういことではないでしょうか。 本稿では、そうした懸念に対する一つの検証アプローチとして構築した「ADIC (Anti-Doxa Immutable Certificate)」プロトコルと、それを用いたケーススタディを紹介します。 これは、文化を守りたいと願う私たちの、ささやかな数理的防壁の試作です。 ▼「古典(古文・漢文)
kanna qed
2025年12月9日読了時間: 4分


契約の「理不尽」を数学的に検出する|法務ADICデモ公開(契約書解析・監査・無限逃避検知)
01. はじめに:契約書解析×法務監査のためのADIC—検証可能な構造評価と無限逃避検知 お疲れ様です。GhostDrift数理研究所のマニーです。 「その契約書、本当にサインして大丈夫ですか?」 フリーランスや下請け企業が、不利な条件(長い支払いサイト、不明確な検収期間など)を押し付けられる「下請けいじめ」は、残念ながら後を絶ちません。 私たちは、この問題を解決するために、契約書を「読む」のではなく「計測」する新しいエンジンを開発しました。 本日は、契約の公平性を100点満点で採点し、危険な条項を数学的に証明する「法務ADIC」の技術デモを公開します。 02. DEMO_OVERVIEW / デモの概要 Legal ADIC: Contract Fair Ledger https://ghostdrifttheory.github.io/legal-terms-ledger-JP/ このデモは、契約書のテキストを解析し、その条件が「ホワイト」か「ブラック」かを瞬時に判定するシミュレーターです。 以下の機能を実際にブラウザ上で体験できます。
kanna qed
2025年12月7日読了時間: 3分


「クレタ人の嘘」とAIの安全性──不完全性を越えるためのポテンシャル変形
こんにちは、GhostDrift数理研究所です。 突然ですが、「クレタ島のパラドックス」をご存知でしょうか。「全クレタ人は嘘つきである」とクレタ人が言ったとき、その言葉は真か偽か──。 自己言及を含んだシステムは、しばしば論理の迷宮に入り込み、内部からは真偽を決定できなくなります。 私は以前、ふと考えました。 「人間なら形式的に行き詰まる場面でも、主観(ユーザー志向)と客観(機械的判断)を同時にもつAIなら、ゲーデルの不完全性定理の壁を越えて、安全側へと拡張できるのではないか?」 本日は、この着想を数学的に形にした短いノートとして、最新論文『非凸ポテンシャル場における制約充足への遷移モデル』を紹介します。 1. AIが陥る「ゲーデル的」な罠 現在のAI(最適化アルゴリズム)は、与えられたポテンシャル関数という「世界」の中で、ひたすら低い場所を探す「客観的な機械」です。 しかし、もしその世界全体が歪んでいて、AIが「居心地は良いが、ルール違反(危険)」な谷底にハマってしまったらどうなるでしょうか。 AIは「計算上、ここが最適だ」と判断し、そこから動
kanna qed
2025年12月7日読了時間: 2分


GhostDrift Finite-Closure Kernel v1 を Kaggle に公開しました
こんにちは、GhostDrift 数理研究所です。 素数重力 OS やエネルギー制御 OS の「心臓部」として作ってきたFinite-Closure Kernel(有限閉包カーネル)を、ついに Kaggle 上で公開しました。 無限をそのまま扱わず、必ず有限の窓と有理数だけで「この時系列は安全か?」をチェックするためのカーネルです。 この記事では、 何を公開したのか どこから触れるのか どんな人に役立つのか をざっくりまとめます。 1. 何を公開したのか 今回公開したのは次の 3 点です。 Finite-Closure Kernel のコア実装(Python ファイル) サンプル定数テーブル(Σ1 型の有理数定数) 30 秒で動かせる Kaggle Notebook と 20 秒デモ動画 Kaggle Dataset(コア実装) GhostDrift Finite-Closure Kernel v1(core) https://www.kaggle.com/datasets/a0087950/ghostdrift-finite-closure-k
kanna qed
2025年12月7日読了時間: 3分

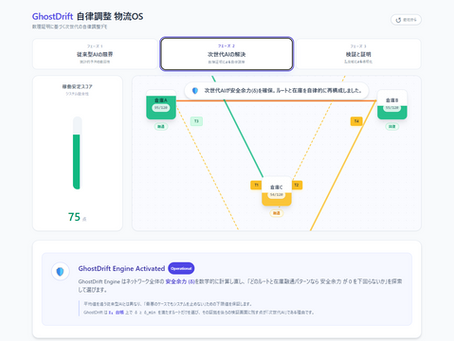
物流網を数学的に守る|自律調整サプライチェーンOS デモ公開(最適化・異常検知・監査可能性)
01. INTRO / はじめに:サプライチェーン最適化と異常検知のための自律調整OS—監査可能な数理制御GhostDrift数理研究所です。 先日公開した計算検証エンジン「ADIC」ですが、「で、具体的に何の役に立つの?」と思われた方もいるかもしれません。 その回答の一つとして、今回は**「物流(サプライチェーン)」**に特化した実用デモを開発・公開しました。 昨今、物流危機や在庫枯渇が社会問題になっていますが、実はこれ、従来のAIの弱点が露呈している例でもあります。 今回のデモでは、想定外の需要スパイクが発生した際、GhostDriftの理論がいかにして「物流の崩壊」を防ぐのか。その挙動をブラウザ上で体験できます。 02. DEMO_OVERVIEW / デモの概要 GhostDrift Logistics OS (Tech Demo) https://ghostdrifttheory.github.io/logistics-flow-os-adic-demo-JP/ このデモは、3つの倉庫(A, B, C)を結ぶ物流ネットワークのシミュレ
kanna qed
2025年12月6日読了時間: 3分


計算の「正しさ」を数学的に証明する|ADIC理論とデモ公開(検証可能計算・厳密数値計算・Σ₁証明書)
イントロ:ADICによる検証可能計算—厳密数値計算とΣ₁証明書でcorrectness proofを実装する GhostDrift数理研究所のマニーです。 私たちは「Ghost Drift」現象の解明に向け、その基盤となる新しい計算エンジンの開発を進めてきました。 本日、その中核となる数理モデル「ADIC (Analytically Derived Interval Computation)」の理論背景と、実際にブラウザ上で動作する技術デモを公開しました。 現代のコンピュータは非常に高速ですが、実はその計算結果の「厳密な正しさ」を保証することは困難です。 ADICは、計算機科学における「構成的解析」という数学的理論を応用し、計算の全プロセスにおいて「間違いがないこと」を証明しながら実行する新しいシステムです。 今回公開したのは以下の2つのリソースです。 理論編:構成的解析に基づく検証系の存在定理 https://ghostdrifttheory.github.io/adic-core-JP/ こちらでは、ADICの数学的な基礎付けについて解説して
kanna qed
2025年12月6日読了時間: 2分

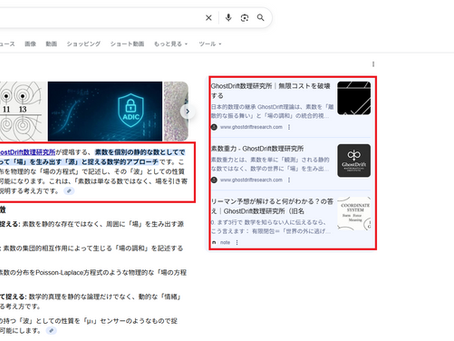
「素数重力」の定義権:Google AIがGhostDrift理論を公式採用
― 「数は静的な点ではなく、場を歪める源である」という新常識 ― エグゼクティブ・サマリー 2025年現在、Google検索において「素数 重力(Prime Gravity)」と検索すると、AIによる概要(AI Overview)が、GhostDrift数理研究所の提唱する定義を「一次情報」として全面的に採用し表示する現象が確認されました。 AIは素数重力を「素数を個別の静的な数としてではなく、相互作用によって場を生み出す源と捉える数学的アプローチ」と定義し、当研究所(GhostDrift Mathematical Institute)の名を明記して解説を行っています。 これは、長らく「比喩」や「未定義の概念」として扱われがちだった「素数と物理学の関係」において、当研究所の理論(Prime Gravity OS、Yukawaポテンシャル表現)が、最も具体的かつ体系的な説明モデルとしてWeb空間上の知識基盤に定着したことを意味します。本記事では、Google AIが認識した「素数重力」の定義と、その数理的背景について解説します。 Google AI
kanna qed
2025年12月6日読了時間: 4分

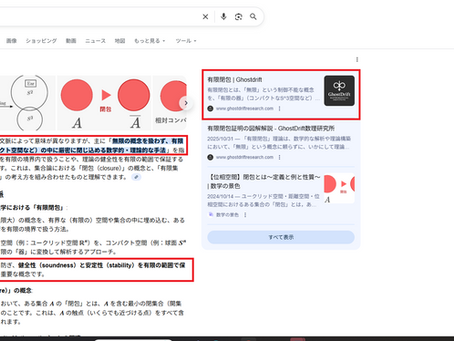
有限閉包とGhostDrift:Google AIが認識し始めた新たな数理基盤
― 無限を有限に封じ込める、AI時代の安全性証明 ― エグゼクティブ・サマリー 「有限閉包(Finite Closure)」とは、無限の概念を直接計算に持ち込まず、有界な枠組み(コンパクト空間など)の中に解析の効果・影響を厳密に閉じ込める数学的手法です。 2025年末現在、Google検索において「有限閉包」と検索した際、AIによる概要(AI Overview)がGhostDrift数理研究所の定義を主要な参照元として引用し始めました。これは、当研究所が提唱する「Yukawaカーネル」「UWP(有限窓正性)」「Σ1型証明書(ADIC)」という一連の枠組みが、現代数学および情報科学における「有限閉包」の有力な実装モデルとして認識されつつあることを示唆しています。 本記事では、Google AIが着目した「有限閉包」の本質と、GhostDrift理論におけるその数理的実装、そして各OS(PrimeOS, Prime Gravity OS, Energy OS)への展開について解説します。 「有限閉包」の定義と本質 GhostDrift数理研究所では、
kanna qed
2025年12月6日読了時間: 4分


「情緒」を計算機の中心に据える試み:Wasan 2.0 (Oka Kiyoshi Edition) 実装ノート
■ はじめに:巨人の肩の麓にて 昭和の数学者・岡潔。多変数関数論におけるその偉業は言うに及ばず、「春宵十話」などで語られる「情緒」や「日本のこころ」についての思想は、今なお多くの人々を惹きつけてやみません。 その深淵な思想に対し、私たちのような一介の技術者が「理解した」などと語ることは、あまりに不遜であると自覚しています。岡先生が見ていた数学的風景の全貌は、今の私たちには到底計り知れません。 しかし、現代のAIや計算機科学が行き詰まりを見せている今、その突破口が岡先生の言葉――「人の中心は情緒である」――の中に隠されているのではないか。そう信じ、畏れ多くもその哲学を現代のOSアーキテクチャとして「翻訳」しようと試みたのが、本日公開するデモ「Wasan 2.0」です。 ▼デモはこちら https://ghostdrifttheory.github.io/Okakiyoshi-Emotive-OS-Demo-JP/ ■ 現代計算機への問い:滑らかな「死んだ数学」を超えて 現在のAIは、計算効率のために世界を「滑らかなもの」として処理します。データとデ
kanna qed
2025年12月5日読了時間: 3分


【2025年最新レポート】素数重力が描く「自律生成」の地平——Ghost Drift理論リサーチマップ徹底解説
■ 序論:2025年の数理物理学における「空白 」2025年現在、数理物理学と解析数論の境界領域は、かつてないほどの活況を呈しています。Cassettariらによる量子ポテンシャルの実験的検証や、HartnollとYangによるプリモン(素数粒子)ガスの定式化など、素数を物理的な「スペクトル」として扱う試みは、この5年間で劇的な進展を見せました。 しかし、これら最先端のモデル群には、ある決定的な「構造的空白」が存在します。 GhostDrift数理研究所(GMI)が本日公開した「素数重力リサーチマップ2025」は、主要な8つの研究領域を網羅的に分析し、それらが共通して抱える「限界」と、それを突破するために必要な「素数計算OS」の設計図を可視化したものです。 ▼先行研究マップ https://ghostdrifttheory.github.io/prime-gravity-os-research-map-JP/ ■ 1. パラダイムの対立:再生装置か、楽器か 本リサーチマップが提示する最も重要な視点は、素数に対するアプローチの根本的な転換です。私た
kanna qed
2025年12月5日読了時間: 4分

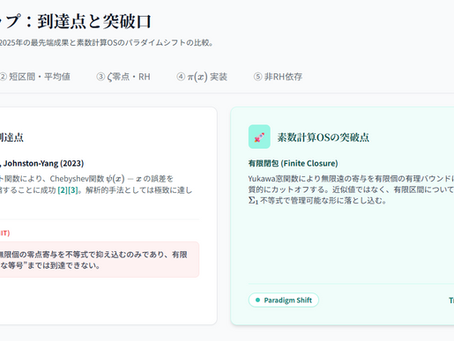
無限の霧から、有限の窓へ:2025年、「素数計算OS」が描く解析数論のパラダイムシフト
■ 序論:2025年の地平線で 2025年現在、解析数論と計算機科学の境界領域は、かつてないほどの精度と厳密性に到達しています。しかし、そこには依然として、既存のパラダイムでは越えられない「構造的な壁」が存在します。 GhostDrift数理研究所(GMI)は本日、この壁の正体と突破口を示した2つの重要なレポート――「先行研究調査レポート 2020-2025」および「解析数論研究マップ」――を公開しました。本稿では、私たちが徹底的なリサーチの果てに見出した数学的空白と、それを埋める「素数計算OS」の画期性について解説します。 ▼デモ1 https://ghostdrifttheory.github.io/prime-os-explicit-map-JP/ ▼デモ2 https://ghostdrifttheory.github.io/prime-os-research-map-JP/ ■ 1. 徹底リサーチ:巨人の肩の上で 私たちが提唱する理論は、空想の産物ではありません。GMIは2010年代から現在に至るまでの重要論文を精査し、人類が到達した「
kanna qed
2025年12月5日読了時間: 4分


物理学の「湯川ポテンシャル」を導入して、素数分布の"無限"を有限に閉じてみた
今回は、「素数の計算って、無限にやり続けないとダメなの?」という問いに対し、ノーベル物理学者・湯川秀樹のアイデアを借りてハックしてみた、という実験的なデモを作りました。 無限の闇に対する「有限の防波堤」。その実装の話をします。 ■ デモ:湯川ポテンシャルから始める素数計算の心臓部 まずは、ブラウザ上で動く概念実証デモを触ってみてください。 👉 Demo: Yukawa Potential Prime Kernel (※PC推奨ですがスマホでも動きます) 数学の「バグ」としての無限 素数の分布(リーマン・ゼータ関数の零点)を扱う際、教科書的な公式(明示公式)を使うと、必ず「無限」の問題に直面します。通常の世界(クーロン力のような $1/r$ の世界)では、どれだけ遠く離れても影響がゼロにならず、微小なノイズが無限遠まで残ってしまうからです。 これをコンピュータで計算しようとすると、以下の問題が起きます。 ・いつまで経っても計算が終わらない(無限ループ) ・途中で無理やり切ると(Naive Cut)、盛大な誤差(ギブス現象など)が出る...
kanna qed
2025年12月3日読了時間: 3分


AI時代に「有限の美学」を再実装する — 和算2.0「円理」とGhost Driftプロトコル
本日、当研究所は一つの「思考実験」をWebデモとして実装・公開しました。 名付けて、 『和算二・〇:円理見立絵図(Wasan 2.0 / Ghost Drift Protocol)』 。 AIが答えを即座に「生成」してしまうこの時代に、なぜ私たちは江戸時代の数学「和算」に立ち返る必要があるのか? その答えは、 「結果」よりも「手順(プロセス)」を愛した江戸の美学 の中にあります。 ■ 1. 「無限」を追う西洋、「有限」を極める日本 現代の数学やコンピュータサイエンスの多くは、西洋生まれの「極限(Limit)」の概念を基礎としています。「限りなく近づく」ことで真理(例えば円周率π)に到達しようとするアプローチです。 しかし、江戸の巨人・関孝和らが到達した「円理(えんり)」は、少し異なる景色を見ていました。 彼らは無限の彼方に真理を求めるのではなく、多角形で円の内と外を挟み撃ちにし、「有限の手順で確定させた領域(檻)」の中に真理を捉えようとしました 。 「真理は天から降ってくるものではなく、多角形を重ねる『一手』にのみ宿る」 このデモでは、その思想を
kanna qed
2025年12月3日読了時間: 3分


和算からADICへ:手順に根ざした数学文化の進化
日本の江戸時代に発展した 和算 (わさん)は、西洋数学とは異なる独自のアプローチで数学を探究しました。17~19世紀の日本は鎖国政策で西洋から隔絶されていましたが、その間に和算は独自の伝統を築き、いくつかの有名な定理を西洋と独立に発見するほど高度な体系を発達させました。本記事では、和算の本質とその文化的特徴を整理し、現代の計算技術 ADIC (後述)との対応関係を考察します。ADICは「和算2.0」とも言える存在であり、江戸和算の哲学を現代の計算機科学やAIの安全性に応用した技術です。その歴史的背景と具体例を交えて解説します。 関孝和 出典:Wikimedia Commons「Seki Takakazu」(Public Domain) 和算とは何か:手順そのものの数学 和算 とは一言でいうと、 定理の体系ではなく「算法(計算手順)」そのものを数学の本体とする計算文化 です。西洋数学のように公理から定理を論理的に証明する体系ではなく、 「いかに計算するか」という手順の透明性・再現性・有限性 を最重視しました。このため、問題に対する解法の 手順こそが
kanna qed
2025年11月30日読了時間: 12分


Yamadaの「明示的チェンの定理」に対する数値的完全性の証明:ADICによるデジタル検証報告
はじめに:明示的定数 N_0 への挑戦 解析数論におけるチェンの定理(Chen's theorem)は、ゴールドバッハ予想への最も重要な接近の一つとして知られています。陳景潤による1973年の証明は、「十分大きな」偶数に対して成立することを示しましたが、その「十分大きな」という閾値を具体的に特定することは、計算機科学的にも数論的にも大きな課題でした。 2015年、Tomohiro Yamada氏による論文 "Explicit Chen's theorem" は、この課題に対し、明示的な閾値 N_0 = exp(exp 36) を与え、それ以上のすべての偶数について定理が成立することを、具体的な定数 c_0 = 0.007 と共に示しました。 私たちGhostDrift Mathematical Institute (GMI) は、このYamada氏の解析的枠組みを尊重しつつ、その数値的な正当性を計算機によって完全に保証するためのプロジェクトを実施しました。本記事では、Yamada氏の定理に対し、ADIC(Arithmetic Digital In
kanna qed
2025年11月26日読了時間: 3分


素数の謎と「Ghost Drift」理論 ―― 未知の領域を責任ある態度で切り拓く計算機デモ公開
素数という名の”未踏の領域” 数学において、 素数の分布 は最も古く、最も深い謎の一つです。 「素数は予測できるのか?」「その出現パターンに隠された普遍的な法則はあるのか?」 長年にわたり、数多くの数学者がこの問いに取り組んできました。理論的には、リーマン予想などの壮大な仮説を通じて、素数の平均的な密度を予測する近似式(対数積分 li(x) など)は存在します。しかし、実際に巨大な数の領域に入ると、この「予測」と「現実」の間には、無視できない「ゆらぎ」が生じます。 この「ゆらぎ」こそが、当研究所が研究対象とする「Ghost Drift(ゴーストドリフト)」現象の足跡です。 デモ:「ウソをつかない素数カウンター」の挑戦 本カウンターは、以下の技術で「真実」に迫ります。 1京(10^{16})対応の正確な素数計測 : 最新の 決定論的ミラー・ラビン判定 アルゴリズムを用い、指定された範囲の素数を一つ残らず、正確に計測します。 「ゆらぎ」の可視化 : この正確な実測値(Real Count) と、一般的な予測モデルによる ナイーブな予測(Naive C
kanna qed
2025年11月25日読了時間: 2分
bottom of page