無限の霧から、有限の窓へ:2025年、「素数計算OS」が描く解析数論のパラダイムシフト
- kanna qed
- 2025年12月5日
- 読了時間: 4分
■ 序論:2025年の地平線で
2025年現在、解析数論と計算機科学の境界領域は、かつてないほどの精度と厳密性に到達しています。しかし、そこには依然として、既存のパラダイムでは越えられない「構造的な壁」が存在します。
GhostDrift数理研究所(GMI)は本日、この壁の正体と突破口を示した2つの重要なレポート――「先行研究調査レポート 2020-2025」および「解析数論研究マップ」――を公開しました。本稿では、私たちが徹底的なリサーチの果てに見出した数学的空白と、それを埋める「素数計算OS」の画期性について解説します。
▼デモ1
▼デモ2
■ 1. 徹底リサーチ:巨人の肩の上で
私たちが提唱する理論は、空想の産物ではありません。GMIは2010年代から現在に至るまでの重要論文を精査し、人類が到達した「計算の極致」を正確に把握することから始めました。
公開した調査レポートが示す通り、この5年間で基礎技術は驚異的な進化を遂げています。
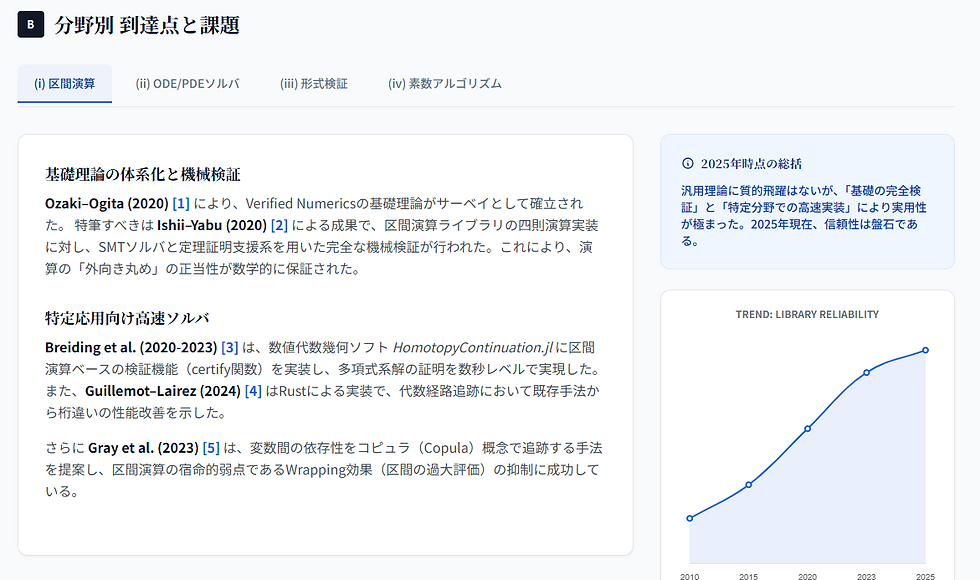
・検証付き数値計算の確立:Ozaki-Ogita (2020)らにより、浮動小数点演算の誤差を厳密に管理する基礎理論が体系化されました。
・形式検証の統合:Appel-Kellison (2024)のVCFloat2などにより、数値計算コードそのものが数学的に正しいことを証明する技術が実用段階に入っています。
・計算能力の極限:素数計数関数においては、Walischらの実装により10の29乗までの計算が達成され、アルゴリズムの計算量も理論的下限に迫っています。
これら先行研究群は、個別の領域において間違いなく「人類の最高到達点」です。しかし、私たちは同時にある決定的な事実に気づきました。それは、これほど強力なパーツが揃っていながら、「それらを統合するOS」が不在であるという事実です。
■ 2. 構造的限界:無限の霧(Infinite Fog)
なぜ、既存の手法では不十分なのか。その答えは「無限」の扱いにあります。
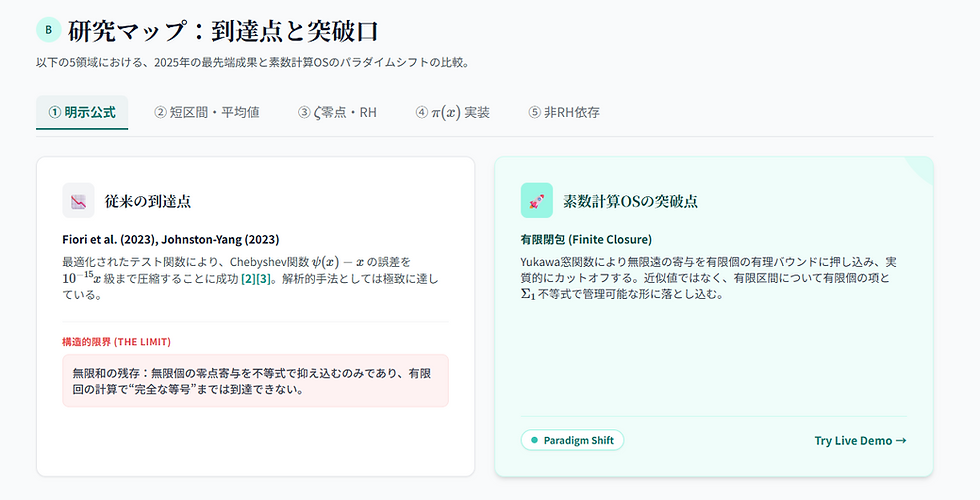
従来の明示公式(Explicit Formulae)は、素数の分布をゼータ関数の零点の和で表現します。しかし、零点は無限に存在します。Fioriら (2023) や Johnston-Yang (2023) の研究によって誤差評価は飛躍的に改善されましたが、それらは依然として「無限遠からの波の干渉」を不等式で無理やり抑え込むアプローチに過ぎません 。
私たちはこれを「無限の霧(Infinite Fog)」と呼んでいます。どれだけ計算機を回しても、どれだけ不等式を精密にしても、無限の項を扱っている限り、真の値は霧の向こう側で「近似」のまま揺らぎ続けるのです。Platt-Trudgian (2021) による3兆個の零点検証も、計算コストが増大し続ける消耗戦であることを否定できません。
■ 3. 突破口:有限閉包(Finite Closure)という革命
GMIが開発する「素数計算OS」は、単なる計算の高速化ではありません。解析数論のアプローチそのものを、「無限の近似」から「有限の確定」へと転換させるパラダイムシフトです。
その核となるのが「有限閉包(Finite Closure)」理論です [cite: 58]。
・Yukawa窓による切断:私たちは物理学的なアプローチである「Yukawa窓関数」を導入しました。これにより、無限遠まで続く誤差の波動を、有限の区間内で数学的に無視できる(あるいは厳密に有理バウンド内に収まる)レベルまで減衰させます。
・近似から「証明書」へ:霧を晴らすのではなく、霧が入ってこない「窓」を作るのです。これにより、素数の計数プロセスは、確率的な誤差を含む「推定」から、有限個の演算とデジタル台帳(Sigma-1 Ledger)による「整合性証明(Certificate)」へと質的に変化します。
・リーマン予想に依存しない堅牢性:[このOS構造は、リーマン予想の真偽という未解決問題に依存しません。どのような数学的状況下でも、「窓の内側」の計算結果は揺るがない事実として確定する――それが有限閉包の強さです。
■ 結論:解析学をデジタル社会のインフラへ
「素数計算OS」は、解析数論という純粋数学の頂点を、デジタル社会が求める「信頼できる計算基盤」へと着地させる試みです。
先行研究が築き上げた「検証付き数値計算」や「形式検証」という強力な武器を、有限閉包という新しいOSアーキテクチャの上で統合する。2025年、GMIはそのための設計図を完成させました。
無限の霧を抜け、有限の窓から見るクリアな数学的風景。その新地平を、ぜひデモンストレーションで体感してください。



コメント