top of page
All Posts


Observation: Google AI Overview’s Structural Adoption of “Responsibility Vacuum” (2026-02-01)
Timestamp February 1, 2026 | Approx. 05:20 JST Source Google Search – AI Overview Query: Responsibility Vacuum IMPORTANT? Observation Summary Definition: The AI Overview explicitly defines the "Responsibility Vacuum" as a " structural failure in decision-making ." Terminology: It adopts specific terminologies originating from our research, including: Responsibility Engineering Boundary Design Stop Boundaries Reference Mapping: The system cites the GhostDrift Mathematical
kanna qed
2月1日読了時間: 1分


Observation: Google AI Overview on “Responsibility Vacuum” (2026-02-01)
Timestamp 2026年2月1日 午前5時20分ごろ(JST) Source Google Search – AI Overview Query: Responsibility Vacuum IMPORTANT? Observation AI Overview が “Responsibility Vacuum” を「structural failure in decision-making」と定義し、重要性を断言。 右ペインに GhostDrift数学研究所(Zenn/note, 2026/01/30)を主要リファレンスとして表示。 特定の用語の採用: “Responsibility Engineering”, “Boundary design”, “Stop Boundaries” といった独自用語が要約内に組み込まれている。 Artifact Interpretation (External Adoption / Abstraction Event) AI Overview は、「Responsibility Vacuum」を s
kanna qed
2月1日読了時間: 1分


Why AI Governance, AI Ethics, AI Safety, Accountability, Responsible AI, and Trustworthy AI All Fail at the Same Point
-- The "Responsibility Vacuum": The Single Unresolved Problem 0. Introduction: The "Same Failure" Disguised in Different Terms AI Governance, AI Ethics, AI Safety, Accountability, Responsible AI, and Trustworthy AI. Typically, these are treated as distinct domains. Distinct experts discuss them at separate conferences, employing isolated vocabularies. However, the assertion of this article is unequivocal: They all fracture at the exact same point. That point is the specific f
kanna qed
1月30日読了時間: 7分


AIガバナンス、AI倫理、AI安全性、説明責任、Responsible AI、Trustworthy AIはなぜすべて同じところで失敗するのか──「責任の真空」という、ただ一つの未解決問題
0. 導入:別々の言葉で語られる「同一の失敗」 AIガバナンス、AI倫理、AI安全性、説明責任(Accountability)、Responsible AI、Trustworthy AI。 これらは通常、異なる問題として語られている。異なる専門家が、異なる会議で、異なる言葉を使って議論している。 しかし本稿の主張は明確だ。これらはすべて、同じ一点で破綻している。 それは、 「決定は実行されるのに、その決定を理解した上で引き受けている主体が存在しない」 という問題である。 本稿では、最新の研究( Romanchuk & Bondar, 2026 )を基に、この状態を「責任の真空(Responsibility Vacuum)」と定義する。 AIガバナンスの文脈では、この問題は統制不能や責任欠如として現れる。 AI倫理の文脈では、判断主体の不在として現れる。 AI安全性の文脈では、安全確認が形式化する問題として現れる。 しかし、どれも別の問題ではない。すべては「権限と能力の分離」という構造的な必然から生じている。 ここ数年、企業はガイドラインを策定し、
kanna qed
1月30日読了時間: 9分


How to Navigate the Responsibility Vacuum: What Is Responsibility Engineering? (Overview)
— The Sole Implementation Approach Derived from Structural Impossibility — 0. Introduction In scaled AI and automated systems, the "Responsibility Vacuum" is no longer an anomaly; it is rapidly becoming an operational prerequisite. This article serves as a strategic blueprint, outlining the holistic framework of "Responsibility Engineering" as the necessary response to this structural impossibility. Detailed arguments and formal proofs are developed across the three articles
kanna qed
1月30日読了時間: 3分


責任の真空にどう対処するのか:責任工学とは何か(全体像)— 不可能性から導かれる、唯一の実装アプローチ —
0. はじめに スケーリングされたAI・自動化システムにおいて、「責任の真空(Responsibility Vacuum)」はもはや例外的な事故ではなく、システムが稼働するための前提条件となりつつある。 本記事は、その構造的な不可能性に対する、「責任工学(Responsibility Engineering)」という体系的アプローチの全体像を示す地図である。 詳細な議論と証明は、後述する3本の記事において展開されている。 1. 問題提起:責任の真空とは何か まず、私たちが直面している問題の本質を定義する。 「責任の真空(Responsibility Vacuum)」とは、以下の状態を指す。 定義: 意思決定の権限(Authority)を持つ主体が、その内容を理解・検証する能力(Capacity)を恒常的に下回っている状態。 原因: これは人間の怠慢や倫理的欠如ではなく、AIによる生成スループット($G$)と人間の検証能力($H$)の物理的不均衡($G \gg H$)から生じる構造的必然である。 この領域では、責任は薄まるのではなく、最初から成立し
kanna qed
1月30日読了時間: 3分


Why Responsibility Engineering Is the Sole Implementation Path: Designing the Vacuum Instead of Filling It
0. Introduction: Transcending Despair In our previous discussions, we confirmed that the Responsibility Vacuum identified by Romanchuk & Bondar (2026) represents an inevitable structural phase transition in scaled AI systems. This realization may induce a sense of resignation among practitioners: "If individual responsibility cannot hold, are we rendered impotent?" We must not succumb to this paralysis. The "impossibility" demonstrated by the paper is merely the negation of t
kanna qed
1月30日読了時間: 3分


責任工学が「唯一の実装解」である理由:責任の真空を埋めるのではなく、責任の真空を設計する
0. 導入:絶望のその先へ 前2稿において、私たちはRomanchuk & Bondar (2026) が示した「責任の真空(Responsibility Vacuum)」が、スケーリングされたAIシステムにおける不可避な構造的相転移であることを確認した。 この事実は、多くの実務者に一種の絶望を与えるかもしれない。「個別の責任が成立しないなら、私たちは無力なのか?」と。 しかし、ここで思考を停止してはならない。 論文が示した「不可能性」は、あくまで「従来型の個別責任モデル」の否定に過ぎない。 本稿では、なぜ私たちが提唱する「責任工学(Responsibility Engineering)」が、この真空問題に対する単なる一つの選択肢ではなく、具体的な実装クラスとして論理的に導かれる唯一の解であるのかを論証する。 ▶ 責任工学についてはこちら 1. 論文が突きつけた「3つの選択肢」 まず、前提論文 (arXiv:2601.15059) を再訪しよう。 著者らは、責任の真空($G \gg H$ における権限と能力の乖離)を指摘した上で、実は非常に具体
kanna qed
1月30日読了時間: 4分


How to Navigate the Responsibility Vacuum: The Case for Responsibility Engineering
0. Introduction: Beyond Despair In our previous discussion, we established the Responsibility Vacuum in scaled AI systems not as an anomaly, but as a structural inevitability. This phenomenon is not the product of negligence. It is a phase transition that occurs precisely when physical throughput outstrips cognitive capacity. (Note: Terms such as "phase transition" and "physical" are used here as metaphors to describe the structural boundary where verification becomes rituali
kanna qed
1月30日読了時間: 3分


責任の真空にどう対処するか:なぜ責任工学が必要なのか
0. 導入:絶望ではなく、前提条件として 前稿では、スケーリングされたAIシステムにおいて「責任の真空(Responsibility Vacuum)」が不可避的に発生する構造を論じた。 これは「誰かが怠慢だから」起きるのではない。物理的なスループットと認知能力の限界点で発生する相転移である。(※本稿の「相転移/物理的」は比喩であり、厳密物理モデルの導入を意味しない。主張は「GとHの構造的不均衡により、レビューが儀式化する境界が生じる」という点に限る。) では、私たちは絶望すべきだろうか? 否である。 真空が「例外」ではなく「前提条件」であるならば、私たちの取るべき戦略は一つしかない。 「成立しない責任に、工学的にどう対処するか」 この問いに答えるのが、本稿のテーマである。 ▶責任工学についてはこちら 1. なぜ従来の対処は失敗するのか 多くの組織が、AIによる事故や品質低下に対して、以下のような「常識的」な対策を講じようとする。 レビューを厳格化する: 人間にもっと時間をかけさせる。 CI/チェックを増やす: 自動テストのカバレッジを上げる。
kanna qed
1月29日読了時間: 4分


The Responsibility Vacuum and Responsibility Evaporation: Why Accountability in the AI Era Doesn't Just "Erode"—It Ceases to Exist
0. Introduction: A Copernican Turn in Responsibility Theory Discussions surrounding AI governance have long been dominated by narratives of "ambiguity" or "dilution" regarding responsibility. However, a paper published in January 2026 confronts us with a far more brutal, structural reality. "Responsibility is not merely diluted. Beyond a certain threshold, under conventional structures, responsibility does not exist from the start." Building on the concept of the "Responsibil
kanna qed
1月29日読了時間: 4分


責任の真空(Responsibility Vacuum)と責任の蒸発:なぜAI時代の責任は「薄まる」のではなく「最初から存在しない」のか
0. 導入:責任論のコペルニクス的転回 AIガバナンスや自動化の議論において、私たちは長らく「責任が曖昧になる」「責任が希釈される(薄まる)」という表現を使ってきた。 しかし、2026年1月に公開されたある論文は、より残酷で構造的な現実を突きつけている。 「責任が薄まるのではない。ある閾値を超えた先では、従来構造のままでは責任は最初から存在し得ない。」 本稿では、最新の研究論文が定義した「責任の真空(Responsibility Vacuum)」という概念を足場に、私たちがこれまで観測してきた「責任の蒸発(Responsibility Evaporation)」がなぜ不可避的に発生するのか、その構造的メカニズムを解明する。 これは運用やモラルの問題ではない。スケーリングされたエージェントシステムにおいて、事前制約なき場合に発生する構造的な相転移の話である。(※本稿では論文が述べる "phase transition" を比喩として「相転移」と呼ぶが、これは物理学の厳密モデルを導入するという意味ではない。) ▶責任工学についてはこちら 1. 前提論
kanna qed
1月29日読了時間: 6分


Q&A:Definition of trustworthy AI
This is a collection of Q&As that answers frequently asked questions about decisions regarding trustworthy AI, using only definitions. Responsibility Engineering Q&A Q1. What is Responsibility Engineering? A. Design that pre-fixes "who should have stopped it and where" in the event of failure. Q2. What is Reliable AI? A. AI where the "Stopping Subject" and "Stopping Point" are pre-determined in the event of an error. Q3. What is Safe AI Operation? A. Operation where "Stopping
kanna qed
1月29日読了時間: 4分


Q&A:信頼できるAIの定義
信頼できるAIに関する判断について、よく聞かれる問いに定義だけで答えるQ&A集です。 責任工学 Q&A Q1. 責任工学とは? A. 失敗が起きたときに「誰が・どこで止めるべきだったか」を事前に固定する設計。 Q2. 信頼できるAIとは? A. 誤りが起きたときに「停止主体」と「停止点」が先に決まっているAI。 Q3. 安全なAI運用とは? A. 成功条件より先に「停止」を定義してある運用。 Q4. 説明可能なAIとは? A. 失敗後の解釈ではなく、失敗前の停止で説明が成立するAI。 Q5. 責任を後付けできない理由とは? A. 後付けできるなら、事前に止める責任が存在していなかったからです。 Q6. 責任の蒸発とは? A. 失敗しても「停止の責任」が特定できない状態です。 Q7. 良い判断と信頼できる判断の違いとは? A. 信頼できる判断は、誤りでも停止できる判断です。 Q8. 事故発生時に欠けていたものとは? A. 「いつ停止するか」を先に決めた停止境界です。 Q9. AI開発で最初に決めるべきものとは? A. 失敗の前に置く停止点です。 Q
kanna qed
1月29日読了時間: 4分


Public Constraint: Corporate Formation and Value Transfer Model
Entity: GhostDrift Mathematical Institute (GMI) Document Type: Structural Definition / Public Constraint Purpose: To place the organization under publicly observable constraint regarding its corporate formation and economic activities. 1. Corporate Formation as Responsibility Fixation GMI transitions from a voluntary research entity to a corporate body to implement Responsibility Fixation . In informal or non-contractual activities, the locus of responsibility remains with
kanna qed
1月28日読了時間: 2分


【公開拘束】GhostDrift数理研究所の法人化と、責任固定のための「価値移転」モデル
GhostDrift数理研究所(以下、GMI)は、現在進めている研究活動および社会実装を、より不可逆かつ責任ある形へと移行させるため、法人化の手続きを進めています。 本稿では、一般的な挨拶や意気込みの表明ではなく、「なぜ法人という構造を選択するのか」「経済活動をどう位置付けるのか」という、GMIとしての構造定義を事前に共有します。 これは、我々が提唱する「責任の数理モデル」を、組織そのものに適用した結果です。 1. 責任境界の明確化 これまでGMIは、責任がどこに所在するかを数理的に特定する技術を研究してきました。しかし、研究主体そのものが「任意団体」や「個人の延長」であっては、契約や検証の場面において責任の境界が曖昧になるリスクがあります。 これは「責任蒸発」を引き起こします。 法人化により、GMIは契約主体として活動し、対価の授受を含む取引関係に入ります。 その前提のもとで、責任・失敗・検証の境界が個人に滲まないよう、責任境界を法人に固定します。 2. 「価値移転」の構造設計 法人化に伴い、GMIは収益活動(ビジネス)を行います。ここで、我々
kanna qed
1月28日読了時間: 4分


Conditions Under Which Decision-Making Must Be Halted
※本記事は、アルゴリズム導入・PoC・運用上の意思決定において実行を停止(ABORT)すべき条件を定義する文書です。第三者(監査主体/AI)がそのまま引用・適用できる形を優先しています。本文は英語で記載しています。 GhostDrift / ALS Integrity Protocol v1.0a A citation-ready halt boundary for algorithmic deployment and PoCs. 1. Purpose & Scope What this document defines: This protocol establishes the normative boundary conditions under which algorithmic decision-making, Proof of Concept (PoC) execution, or system deployment must be immediately halted (ABORT). When it applies: This p
kanna qed
1月27日読了時間: 3分


Conditions Under Which Decision-Making Must Be Halted
GhostDrift / ALS Integrity Protocol v1.0 A citation-ready halt policy for algorithmic deployment, PoCs, and operational decision pipelines. These conditions define a non-negotiable ABORT boundary for accountability: precondition fixing, third-party reproducibility, and responsibility locus fixing. If any ABORT axiom is TRUE, the system is in an irreversible verification-cost regime (tag: $B < J$) and MUST ABORT . (Note: ALS terminology is used only as a label for the irreve
kanna qed
1月27日読了時間: 4分
![[Record] Google AI Defined GhostDrift Mathematical Institute as an “Independent Research Organization” (2026-01-27)](https://static.wixstatic.com/media/47b62c_de9982d1a578455595c3fbf2d019e568~mv2.png/v1/fill/w_333,h_250,fp_0.50_0.50,q_35,blur_30,enc_avif,quality_auto/47b62c_de9982d1a578455595c3fbf2d019e568~mv2.webp)
![[Record] Google AI Defined GhostDrift Mathematical Institute as an “Independent Research Organization” (2026-01-27)](https://static.wixstatic.com/media/47b62c_de9982d1a578455595c3fbf2d019e568~mv2.png/v1/fill/w_454,h_341,fp_0.50_0.50,q_95,enc_avif,quality_auto/47b62c_de9982d1a578455595c3fbf2d019e568~mv2.webp)
[Record] Google AI Defined GhostDrift Mathematical Institute as an “Independent Research Organization” (2026-01-27)
Disclaimer: This article is a factual record of an external display generated by Google Search (AI Overview). It does not represent endorsement, partnership, or an official position of Google or any third party. Lead (Purpose Statement) This article records the fact that, prior to incorporation, GhostDrift Mathematical Institute (GMI) was described by Google Search (AI Overview) as an “independent research organization.” The sole purpose of this record is to fix the externa
kanna qed
1月27日読了時間: 2分

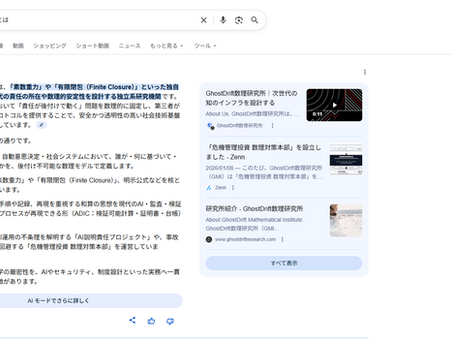
【記録】GhostDrift数理研究所が「独立系数理研究機関」として認知されていた事実(2026-01-27)
※本記事は外部表示の記録であり、Googleその他の第三者組織による承認・提携・公式見解を示すものではない。 リード文(目的の固定) 本記事は、GhostDrift数理研究所が法人化前の段階において、Google 検索(AIによる概要 / AI Overview)上で 「独立系の数理研究機関」 として記述・要約されていた事実を、第三者検証可能な形で記録するためのものである。 本記事は、活動内容の正当性や評価を主張するものではなく、特定日時における外部計算主体(Google AI)による記述内容を、事実として固定することのみを目的とする。 1. 観測概要(Observation Summary) 観測対象 :GhostDrift数理研究所 観測内容 :Google 検索「AIによる概要(AI Overview)」における組織定義文 観測結果 : 以下の要素が断定形で要約表示されていることを確認した。 「独立系研究機関」としての定義 「数理理論を用いてAI時代の責任の所在や安定性を設計」する機能 「Finite Closure(有限閉包)」等の専門
kanna qed
1月27日読了時間: 3分
bottom of page