物理学の「湯川ポテンシャル」を導入して、素数分布の"無限"を有限に閉じてみた

今回は、「素数の計算って、無限にやり続けないとダメなの？」という問いに対し、ノーベル物理学者・湯川秀樹のアイデアを借りてハックしてみた、という実験的なデモを作りました。

無限の闇に対する「有限の防波堤」。その実装の話をします。

■ デモ：湯川ポテンシャルから始める素数計算の心臓部

まずは、ブラウザ上で動く概念実証デモを触ってみてください。

👉 Demo: Yukawa Potential Prime Kernel (※PC推奨ですがスマホでも動きます)

数学の「バグ」としての無限

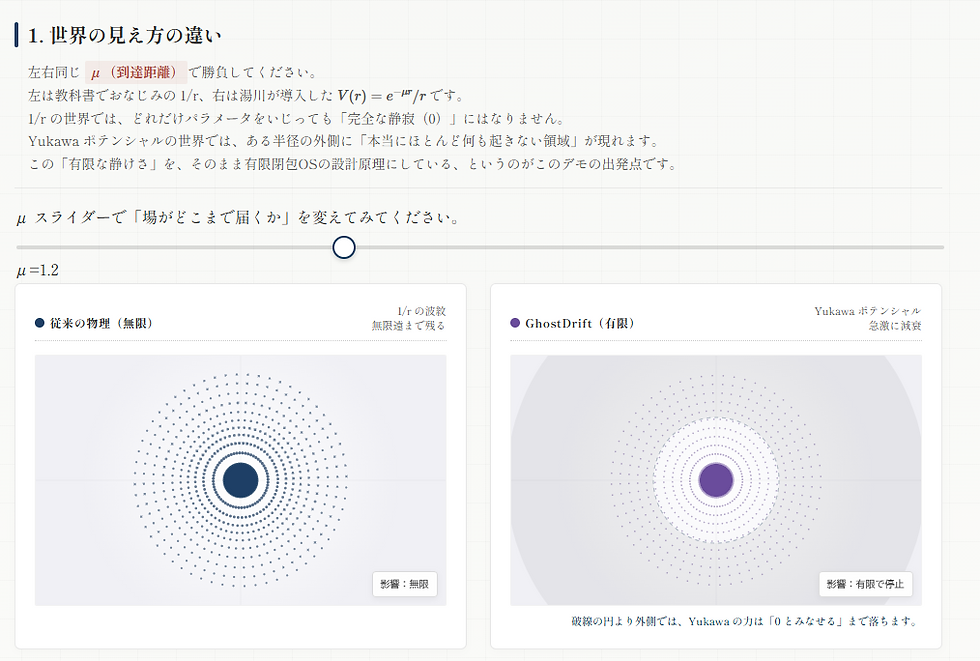
素数の分布（リーマン・ゼータ関数の零点）を扱う際、教科書的な公式（明示公式）を使うと、必ず「無限」の問題に直面します。通常の世界（クーロン力のような $1/r$ の世界）では、どれだけ遠く離れても影響がゼロにならず、微小なノイズが無限遠まで残ってしまうからです。

これをコンピュータで計算しようとすると、以下の問題が起きます。

・いつまで経っても計算が終わらない（無限ループ）・途中で無理やり切ると（Naive Cut）、盛大な誤差（ギブス現象など）が出る

つまり、「有限のリソースで真値を確定させたい」というエンジニアリングの要求と、「無限を見ないと気が済まない」という数学の仕様がコンフリクトを起こしている状態です。

そこで導入するのが、物理学のアイデアです。かつて湯川秀樹は、原子核の中で働く力が「無限に届く」のではなく、「ある距離より外側では急激に減衰して消える」ことを見抜きました。これが「湯川ポテンシャル」です。

この \mu（質量項）があるおかげで、影響範囲は「有限」に閉じ込められます。

今回のデモでは、この物理モデルを「素数解析のカーネル関数」として移植しました。デモ画面の「μスライダー」を動かすと、波紋が遠くまで広がらず、ある半径（Cutoff）でスッと消滅する様子が視覚化されています。

単に「途中で計算をやめる」のと、「影響がなくなったからやめる」のは、似て非なるものです。デモの中段にあるコントロールパネルで、カーネルを切り替えてみてください。

・Naive Cut: ただ途中で切っただけ。誤差が暴れます。

・Yukawa × Fejér (有限閉包): 今回実装した特異なカーネルです。

この「有限閉包カーネル」は、物理的な減衰（Yukawa）と解析的な平滑化（Fejér）を組み合わせることで、「ここで切っても、その外側の誤差は \varepsilon_{\text{safe}} 以下である」と数学的に保証できる地点（有限窓）を作り出します。

無限の宇宙を、ポアンカレ的に「有限の閉じた宇宙」として再定義する試みです。

デモの最下部にあるのが、当研究所が提唱する「ADIC（Arithmetic Digital Integrity Certificate）」のプロトタイプです。

これは、以下の厳格なルールで動く「台帳」です。

この条件が満たされない限り、台帳は「Locked」状態で中身を見せてくれません。

「計算結果」だけをポンと出すのではなく、「計算の正当性が担保された状態」そのものをログとして残す。これは、AIのハルシネーション（もっともらしい嘘）に対する、数理的なアンチテーゼでもあります。

「無限を前提にしなくても、世界は記述できる」

湯川秀樹が愛した東洋的な「足るを知る（有限性）」の思想。それはリソースが限られた現代のコンピュータサイエンスにおいてこそ、再評価されるべきカーネル（核）なのかもしれません。

Ghost Drift数理研究所では、こうした「数理物理 × 実装」のアプローチで、新しい計算の地平を探求しています。