ζ関数の「エネルギー」と「形」:— なぜ解析接続は「形」だけだったのか? 素数重力が「エネルギー」で解き明かすリーマン予想の構造的必然性(5つの図解) —
- kanna qed
- 2025年11月2日
- 読了時間: 4分
イントロダクション
素数は、なぜあんなにも不規則に、それでいて不可解な秩序をもって現れるのでしょうか?
この数学最大の謎を解くため、天才数学者リーマンは「ゼータ関数」という強力な“地図”を作り出しました。この地図は、素数の分布と深く結びついています。
しかし、この地図には「致命的な欠陥」がありました。
リーマン予想が関わる最も重要な領域({Re}(s) <= 1/2$)に足を踏み入れると、地図は「無限大」に発散し、読み取れなくなってしまうのです。(図1参照)
図1:ζ関数は、σ > 1/2(右側)では有限の「波」だが、σ < 1/2(左側)ではエネルギーが発散してしまう。
これまで数学者たちは、この「発散」を「解析接続」という数学的な“パッチ(つぎはぎ)”で修正してきました。それは、破れた地図の「形」だけを滑らかにつなぎ合わせるような、見事な「応急処置」でした。(図3参照)
しかし、その「形」に、物理的な「意味」はあるのでしょうか? 「素数重力(Prime Gravity)」は、まさにこの問いから始まります。
私たち GhostDrift数理研究所(GMI)は、全く新しい視点を提案します。 「もし、ゼータ関数が静的な“地図”ではなく、素数が奏でる“音場(エネルギーの場)”だとしたら?」
この視点に立つと、「発散」はバグではなく、単に「エネルギーが大きすぎて測定器が振り切れている」状態だとわかります。
ならば、必要なのは「解析接続」という数学的な“パッチ”ではありません。 GMIが考案した「有限窓」という、高性能な**“観測装置”**です。(図2参照)
図2:GMIが用いる「有限窓」のイメージ。高性能な測定器のように、近くの信号(局所寄与)は強く捉え、遠くのノイズ(遠方寄与)は自然に減衰させる。
この記事では、たった5つの図を使い、
なぜ従来の「解析接続」が“エネルギー”を殺してしまったのか(図3)
GMIの「素数重力」が、いかにして「生きたエネルギー」を捉えるのか(図2, 図4)
そして、なぜこの「生きたエネルギー」の視点だけが、$\mathrm{Re}(s)=1/2$ の直線上にゼロ点が並ぶ「構造的必然性」を解き明かせるのか(図4, 図5)を、解説します。
5つの図解説明
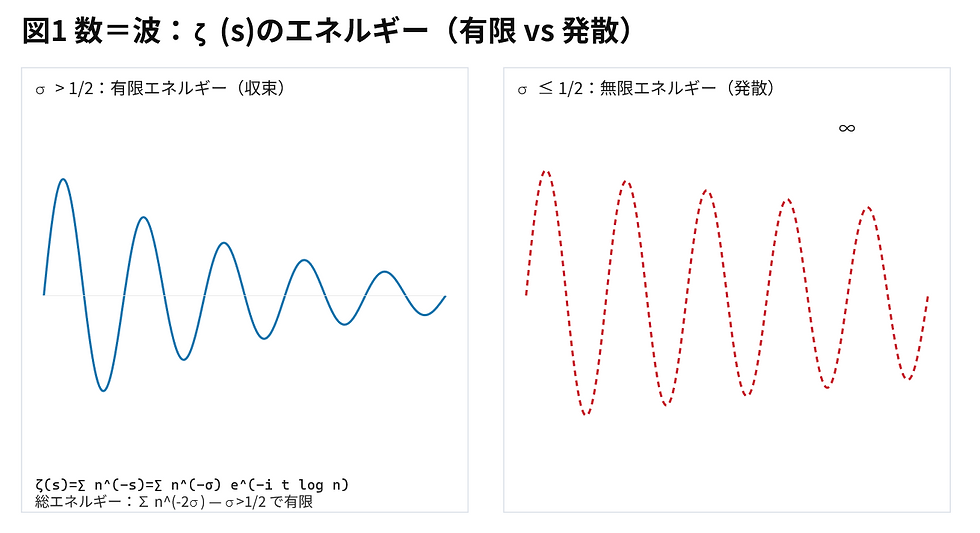
ここでは「数」を静的な記号ではなく、“波としての存在”として描いています。ζ(s) は、1・2・3・4…という数たちが発する無数の波の合成音です。
右側の「σ ≤ 1/2」の世界では、波が減衰せず、遠くまで響きすぎてエネルギーが発散してしまう。
左側の「σ > 1/2」では、波が距離に応じて静まり、有限のエネルギーとして整っている。
つまり、数の世界にも「エネルギー保存の領域」があることを可視化しています。

発散を止める仕組みが「有限窓(Fejér–Yukawa kernel)」です。これは“遠くの影響を自然に減衰させる”フィルター。
近く(中央)では波の力が強く、
遠くにいくほど指数的に弱まる(e^(-λ|x|) の形)
これによって、無限の影響を有限の器に閉じ込めることができます。数学的には正則化ですが、物理的には「距離によるエネルギーの減衰」という極めて自然な現象です。

ここでは、古典的な“解析接続”がどう発散を扱っていたかを示しています。
左側の波は暴走している(エネルギーが無限大)
右側の波は別の関数を使って“形だけ”滑らかに見せている
解析接続とは、数式の形を延命させる操作であり、本来の波のエネルギーや干渉の実体は失われています。言い換えれば、“音は聞こえないけどグラフはきれい”という状態です。
有限窓が「エネルギーを保存する延命」だとすれば、解析接続は「形だけ残す延命」。

ここが素数重力の核心です。
左側:素数はそれぞれ音源(周波数 log p)。
右側:それらの波が重なり合い、**干渉点では“無音”**になる。
この「無音点」が、リーマン予想でいう零点(Re(s)=1/2)に対応します。つまり、リーマン面の真ん中(Beacon)は、“乗法的構造(素数)”と“加法的構造(波の干渉)”が完全に整合する唯一の位置なのです。
これは単なる数の対称性ではなく、エネルギーが完璧に均衡する点。素数が「音の源」であり、加法的調和が「沈黙(ゼロ)」として現れる。数学の中で音楽が鳴り、音楽の中で数学が成立する地点です。

最後の図は、二つの手法の根本的な違いを整理しています。
結論として、有限窓は「形のためにエネルギーを殺さない数学」です。それが**素数重力の根底にある“有限閉包=生きた数理”**という考え方です。
結論
5つの図解で見てきたように、リーマン予想への道は二つありました。
一つは、エネルギー(実体)を捨てて「形」の滑らかさだけを延命させた、従来の**「解析接続」の道。 もう一つは、「有限窓」という物理的な観測装置で「エネルギー」を生かしたまま扱い、「素数=音源」と「干渉=無音」の完璧な一致点(Beacon)を探す、GMIの「素数重力」**の道です。
Re(s)=1/2 という直線は、単なる「対称性の軸」なのではなく、素数が放つ「エネルギー」が完璧に均衡する、唯一の「構造的必然性」の場所なのです。
「形のためにエネルギーを殺さない数学」。 それこそが、「素数重力」の根底にある“有限閉包=生きた数理”という、私たちが提唱する数学の新しい地平です。


コメント